How do batteries change their chemical reaction rates in exactly the right way?
Batteries are constant voltage providers, not constant current providers. The current a battery supplies depends on what it’s connected to. If it’s connected to a low resistance, then it provides a big current, and shifts energy quickly. If it’s connected to a high resistance, then it provides a small current, and shifts energy slowly. In this section we’ll explain how the ideas of current and rate of heating are connected by thinking about what controls the rate of chemical reactions in a battery.
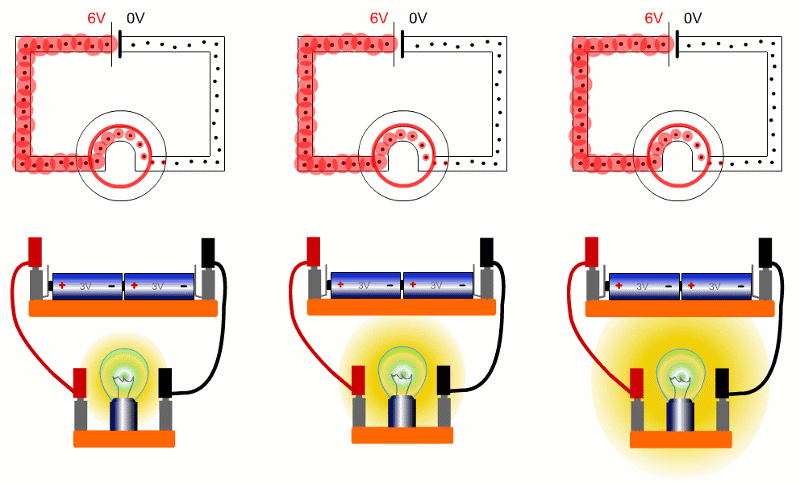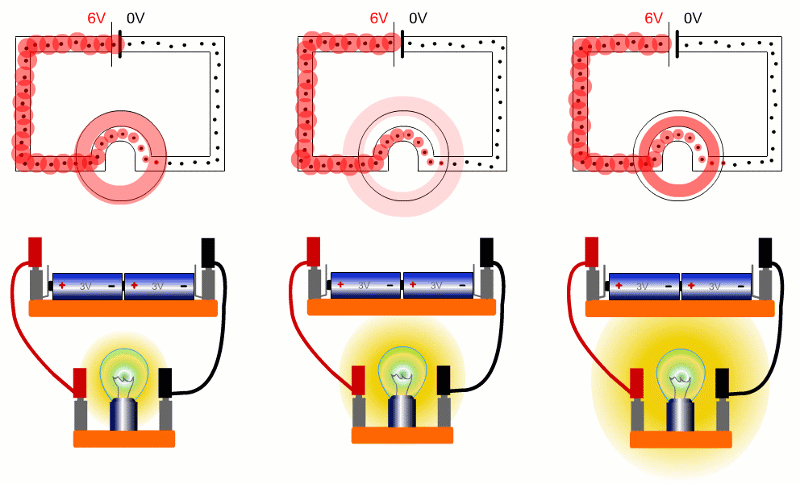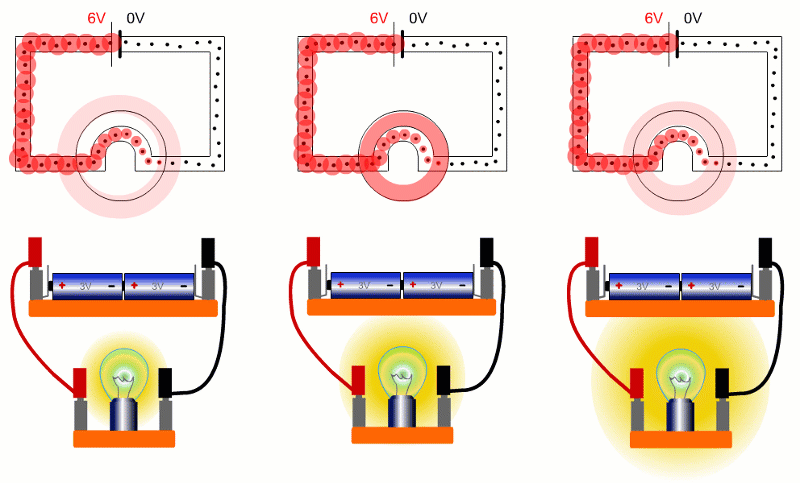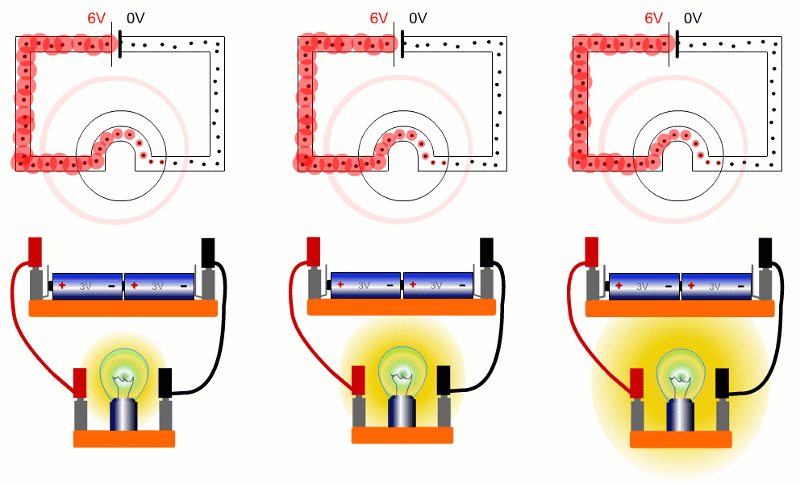
Here are three bulbs with different resistances connected across the same batteries. The bulb on the right has the lowest resistance, so is brightest. Lowest resistance, means biggest current, so energy is shifted from battery to bulb quickest.
Batteries work by chemical reactions that give out electrons at one terminal while taking them in at the other
I’m not going to go into the detailed chemistry of how batteries work, so this is just an outline that’s good enough for our purposes.
Batteries (strictly ‘cells’) work by having two electrodes immersed in a conducting liquid or paste, called on electrolyte. The electrodes are made of different chemical compounds, for example in AA alkaline batteries one is made of zinc and the other is made of manganese oxide. One electrode would like to react with the electrolyte by taking an electron, the other would like to react by giving it an electron. They can do this a little bit, but then the electrodes themselves become very slightly charged so it’s more and more difficult to move the next electron and the reaction stops quickly.
This is the picture of our battery when it’s not connected to anything. It’s got lots of chemicals that really want to react, but they can’t cooperate with each other in a way that allows one electrode to give away its excess electrons to the other electrode which lacks them.
However, if you join the tops of the electrodes together, for example with a wire, then each extra electron on one electrode can shuffle all the free electrons that are already in the wire along by one, and the electron at the end can move onto the electrode that’s given one away. The electrodes themselves stay neutral but now electrons can move round and round the circuit as the electrodes react with the conducting liquid.
If you join the electrodes together with two wires and a bulb then we’ve built ourselves an electric circuit that’s useful.
In this highly simplified visualisation the chemical reactions at the two electrodes are not shown. We’ve also imagined that electrons travel through the potassium hydroxide solution, whereas really the current inside the battery is made of positive and negative ions travelling in opposite directions.
The faster the chemical reactions go, the bigger the current delivered and the faster energy is shifted
There are separate chemical reactions at each electrode. When the electrodes are connected outside the cell then both reactions can run simultaneously. The two reactions together are exothermic. In other words, the reactions happen spontaneously - you don’t have to provide heat - and the reactions themselves cause heating.
What you want is for that heating to happen in your lightbulb filament - which is useful - not in the battery - which isn’t, and that’s the function of the electric current - to relocate where the energy from the chemical reactions appears.
So the chemical reactions in the battery involve two related events:
electrons are made available to flow round the circuit
some energy is liberated as heat in the external circuit
The faster the chemical reactions go, the faster electrons are made available and the quicker heat is liberated. The number of electrons made available per second is a measure of the electric current, and the speed at which heat is liberated is effectively the definition of power.
So if you want a big current and high power, you need fast chemical reactions.
The question is how does the battery ‘know’ when to react faster, and once it does start reacting faster, how does it know exactly what current, and hence what power, it should aim for?
The chemical reactions will go as fast as they can until some factor limits them
The maximum speed the chemical reactions in the battery can go at happens if you simply join the electrodes together at the top outside the electrolyte. In this case what limits the reaction rate will be how often the various randomly moving atoms and ions in the electrolyte can meet another atom or ion they want to react with - this is down to factors like temperature, concentration and surface area.
In this case the electric current and rate of heating will be at their maximum possible values, but all the heating will happen in the battery.
So this is our first assumption - the chemical reactions will happen as fast as they can, until they reach some factor that is limiting the rate.
Once the battery is connected as part of a circuit with something sensible like a bulb, then the limiting factor is found in some property of the bulb filament, not the chemical kinetics of the battery.
It’s very tempting at this point to introduce ideas like resistance and potential difference, but I’m going to try and avoid doing that. Instead, I’m going to offer an explanation only in terms of current and power. There are three reasons for this approach
Current and power are more fundamental ideas than resistance and potential difference. Current is tied up with the idea of electric charge, which is a conserved quantity and electrons, which are fundamental particles. Energy can also be viewed as a fundamental quantity, which is also conserved.
Current and power are meaningful quantities when independently discussing either batteries or bulbs, whereas potential and resistance suggest connections that we’d rather not assume in advance.
If you use derived units you increase the risk that you’ll create an argument that is simply tautologically or trivially true, for example, ‘the fastest sprinter ran the race in the shortest time’
Every type of battery chemistry has a specific power output for any given current it supplies
Every time an electron is made available to the circuit by the chemical reactions in the battery this is associated with a fixed amount of energy. All this energy appears as heating somewhere. The amount of energy is decided by the chemical reactions, and can’t be changed.
We’re interested in how fast the chemical reactions go, and this is directly connected to how fast electrons are made available, and how quickly heating happens - in other words, current and power.
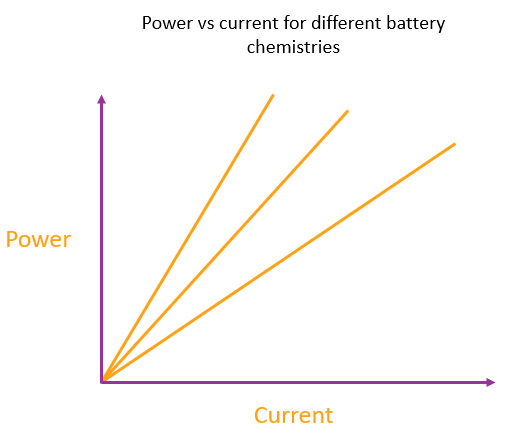
Regardless of why the battery is providing any given current, the amount of heating for that current is always fixed. The current and the heating are directly proportional to each other because a given change in current always gives the same change in power output, so plotting power vs. current will give a straight line through the origin.
We can represent a particular type of battery chemistry (regardless of the battery design or size) by the gradient of this power vs current line. The more energy made available per electron, the steeper the line.
We’re not making any claims yet as to why the current has any given value, but we do know the rate of heating for any current we end up with.
Each line represents a different battery chemistry. The steepest line represents a battery with a chemistry that liberates the most energy per electron made available in the circuit.
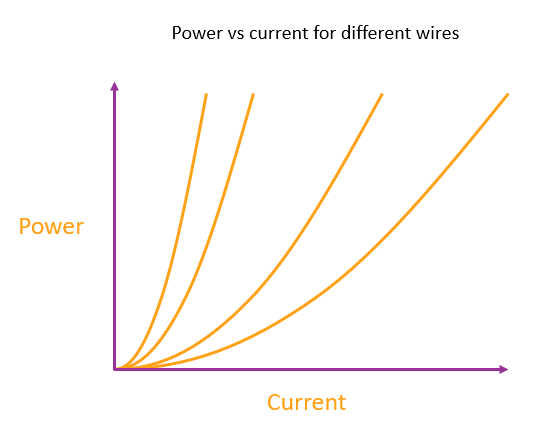
Every wire has a specific rate of heating for a given current flowing through it
When a wire has no current flowing in it then the free electrons move randomly at very high thermal speeds continually interacting with the vibrating atoms of the lattice, and exchanging energy with them. There’s an equilibrium where the electrons, ions and environment all exchange energy at the same rate, and there’s no net energy transfer.
If we push the electrons through the wire - in other words when a current flows - then we’re adding energy to the system (because of the work we do pushing), and so the electron-ion interactions are no longer in thermal equilibrium and the additional energy we put in appears as heating.
The faster we make the electrons move, the faster the heating. In other words, big current means high power.
But is this power directly proportional to the current like it was with the battery? The answer is no.
Power actually depends on current twice.
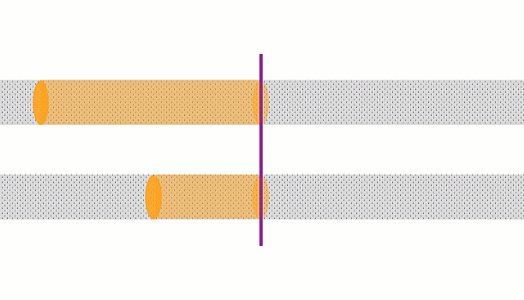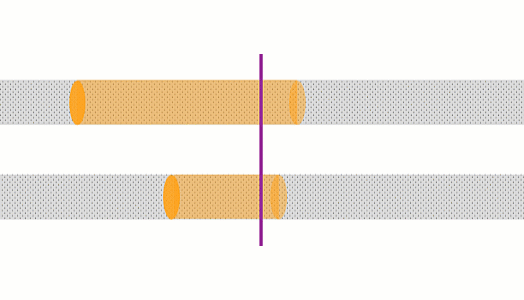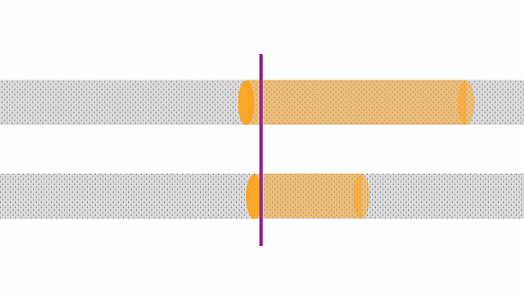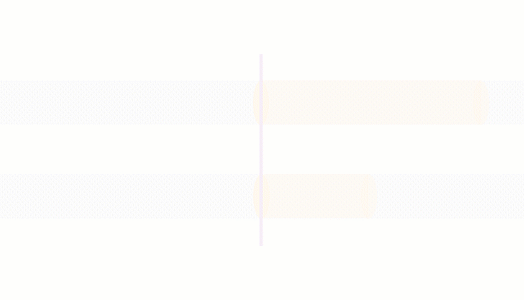
A bigger current means that the imaginary ‘tube’ of electrons that flows past a point in one second is longer, and so there are more electrons in it. The more electrons we’re considering, the greater the rate of heating.
This tube of electrons is also moving faster, so there are more interactions per second between the electrons and the lattice
These animations show the same wire with two different currents. The top animation shows double the current of the bottom one. In the top case, the amount of charge moving past a point in a given time is 2x that of the bottom case, and the charges are moving 2x as fast, so there is 4x the rate of heating.
The rate of heating in a wire depends on the current squared
For a given wire (of any length, thickness or metal), the rate of heating depends on the square of the current.
So the graph of power vs. current for a wire is a parabola through the origin. There are an infinite number of possible parabolas and also an infinite number of possible wires for each parabola, because you can always adjust the length or thickness to give the same rate of heating per ampere.
But for any wire that you choose there is one and only one parabola that corresponds to that particular wire.
Each line represents a different wire. The wires might differ by any combination of length, thickness and metal. The steeper the parabola the more heating for a given current.
For a particular battery and wire, there is only one stable current where the reaction rate is not increasing, and the rate of heating in the wire isn’t greater than the rate of energy liberation in the battery
Remember that there are two iron-clad but distinct relationships
For the battery - any given current it provides must be associated with one and only one rate of energy liberation, because each single reaction involves the transfer of a fixed number of electrons and a fixed amount of energy change.
For the wire - any given current flowing through it must be associated with one and only one rate of heating.
Now let’s think about what happens when we join these two separate ideas - when a given wire is connected across a given battery. (Let’s say the wire is made of a metal and shape so that the current isn’t very big.)
There are two important conservation ideas that can’t be violated
Conservation of charge - the current provided by the battery must be the same as the current flowing in the wire
Conservation of energy - the rate at which the wire is heated can’t be any greater than the rate at which the chemical reactions liberate energy
And we’ll also use the other principle that the battery chemical reactions will go as fast as they can until they bump up against some factor that limits their rate.
Let’s think about it from the battery’s point of view - we are after all trying to explain why the battery’s chemical reaction rate changes, and why it reaches a particular value.
The battery’s initial chemical reaction rate is zero. When the wire is connected, there is suddenly a path for electrons to be shunted from one electrode to the other, and the reaction rate starts to rise rapidly. The same rising current always flows in the battery and wire, but initially most of the energy shifted is still in the battery, because the current in the wire is still low.
However, as the rate of reaction increases it rapidly reaches a current where, if the current increased beyond it, the rate of heating in the wire would be greater than the rate at which energy is liberated in the battery. This would be impossible, since we’d be getting energy out quicker than we put it in, which is a violation of energy conservation.
So there’s this one stable current for the combination of this particular battery chemistry and this particular piece of wire. The rate of reaction has been limited by the rate at which heating can occur in the wire, and so it settles on this value.
Each battery chemistry has its own straight line. Every wire has its particular parabola. There is only one point where the line and the parabola can cross, and that is the value of the stable current for that combination of battery and wire.
For a battery, the gradient of its power vs. current graph is the definition of its voltage
We generally define voltage as joules per coulomb, but we can also divide top and bottom by time to get watts per ampere. This is in fact how the volt is defined - the potential difference when one ampere dissipates one watt of power.
We’re quite comfortable talking about electrons and energy liberated in chemical reactions, but in the 1830s scientists didn’t know about electrons and were only beginning to understand chemistry at an atomic level.
Imagine you were an early scientist and you’d been experimenting with different chemical reactions to make a battery. How would you describe how your battery behaved?
You could measure current using one of the recently invented galvanometers, but you knew that the current depended on what your battery was connected to. You might notice that different batteries caused different amounts of heating for the same current, and if you were around in the 1860s you could measure and define the number of joules of the new-fangled concept of energy were involved in that heating.
So the idea of assigning a number to a battery based on the rate at which it was able to heat something up for a given current, would be both meaningful and measurable.
I’m not arguing incidentally that this is exactly what happened, but simply that defining battery voltage in terms of watts per ampere, rather than joules per coulomb is not as perverse as it might first appear.
A battery can be defined by the gradient of its power vs. current graph. This is what battery voltage means - the power a battery liberates when it supplies one ampere of current.
For a wire, the constant of proportionality that connects rate of heating with current squared is the resistance
We’ve said that for a wire, the graph of rate of heating (power) vs. current is a parabola that goes through the origin.
We can write power ∝ current squared, or
P = k I2
The constant of proportionality k, defines which of the infinite number of curves this particular wire belongs to.
Instead of calling the constant of proportionality k, we attach some physical meaning to it and call it the resistance, R.
So we can write
P = R I2
orP = I2 R
The bigger the value of the resistance, the steeper the parabola, just like
y = 2 x2
is steeper thany = x2
The higher the resistance, the steeper the parabola. This is a purely mathematical observation that the size of the multiple of the squared number determines how steep a parabola is.
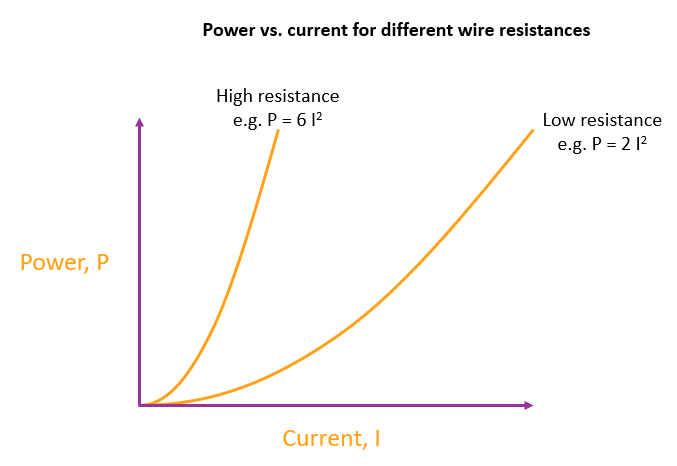
For two resistances connected independently across the same battery, the higher resistance has a lower equilibrium value for current and power
Because high resistance means a steeper parabola for the wire power vs. current curve, the straight line for a battery will cut it earlier than if the parabola was shallower. This is effectively the meaning of resistance - some components have a lower equilibrium current and rate of heating when connected across a particular battery. We imagine components have this property called resistance that when it’s value is high causes the equilibrium current and rate of heating to be small.
As an aside, the battery will also take longer to run out of chemicals (and therefore energy) because high resistances cause the chemical reactions to run slower.
The higher the resistance, the steeper the parabola. The chemical reactions reach a stable value where the battery straight line crosses the parabola for the wire. A high resistance wire cuts the battery line earlier, so high resistance means slower chemical reactions, and so smaller current and lower power